38  高斯过程回归

\[ \def\bm#1{{\boldsymbol #1}} \]

本章主要内容分三大块，分别是多元正态分布、二维高斯过程和高斯过程回归。根据高斯过程的定义，我们知道多元正态分布和高斯过程有紧密的联系，首先介绍多元正态分布的定义、随机数模拟和分布拟合。二维高斯过程很有代表性，常用于空间统计中，而一维高斯过程常用于时间序列分析中，因而，介绍高斯过程的定义，二维高斯过程的模拟和参数拟合。在后续的高斯过程回归中，以朗格拉普岛的核辐射数据为例，建立泊松空间广义线性混合效应模型（响应变量非高斯的高斯过程回归模型），随机过程看作一组存在相关性的随机变量，这一组随机变量视为模型中的随机效应。

38.1 多元正态分布

设随机向量 \(\bm{X} = (X_1, X_2, \cdots, X_p)^{\top}\) 服从多元正态分布 \(\mathrm{MVN}(\bm{\mu}, \Sigma)\) ，其联合密度函数如下

\[ \begin{aligned} p(\boldsymbol x) = (2\pi)^{-\frac{p}{2}} |\Sigma|^{-\frac12} \exp\left\{ -\frac12 (\boldsymbol x - \boldsymbol \mu)^T \Sigma^{-1} (\boldsymbol x - \boldsymbol \mu) \right\}, \ \boldsymbol x \in \mathbb{R}^p \end{aligned} \]

其中，协方差矩阵 \(\Sigma\) 是正定的，其 Cholesky 分解为 \(\Sigma = CC^{\top}\) ，这里 \(C\) 为下三角矩阵。设 \(\bm{Z} = (Z_1, Z_2, \cdots, Z_p)^{\top}\) 服从 \(p\) 元标准正态分布 \(\mathrm{MVN}(\bm{0}, I)\) ，则 \(\bm{X} = \bm{\mu} + C\bm{Z}\) 服从多元正态分布 \(\mathrm{MVN}(\bm{\mu}, \Sigma)\) 。

38.1.1 多元正态分布模拟

可以用 Stan 函数 multi_normal_cholesky_rng 生成随机数模拟多元正态分布。

data {
  int<lower=1> N;
  int<lower=1> D;
  vector[D] mu;
  matrix[D, D] Sigma;
}
transformed data {
  matrix[D, D] L_K = cholesky_decompose(Sigma);
}
parameters {
}
model {
}
generated quantities {
  array[N] vector[D] yhat;
  for (n in 1:N){
    yhat[n] = multi_normal_cholesky_rng(mu, L_K); 
  }
}

上述代码块可以同时模拟多组服从多元正态分布的随机数。其中，参数块 parameters 和模型块 model 是空白的，这是因为模拟随机数不涉及模型推断，只是采样。核心部分 generated quantities 代码块负责生成随机数。

# 给定二元正态分布的参数值
multi_normal_d <- list(
  N = 1, # 一组随机数
  D = 2, # 维度
  mu = c(3, 2), # 均值向量
  Sigma = rbind(c(4, 1), c(1, 1)) # 协方差矩阵
)
library(cmdstanr)
# 编译多元正态分布模型
mod_multi_normal <- cmdstan_model(
  stan_file = "code/multi_normal_simu.stan",
  compile = TRUE, cpp_options = list(stan_threads = TRUE)
)

抽样生成 1000 个服从二元正态分布的随机数。

simu_multi_normal <- mod_multi_normal$sample(
  data = multi_normal_d,
  iter_warmup = 500,    # 每条链预处理迭代次数
  iter_sampling = 1000, # 样本量
  chains = 1,           # 马尔科夫链的数目
  parallel_chains = 1,  # 指定 CPU 核心数，可以给每条链分配一个
  threads_per_chain = 1, # 每条链设置一个线程
  show_messages = FALSE, # 不显示迭代的中间过程
  refresh = 0,        # 不显示采样的进度
  fixed_param = TRUE, # 固定参数
  output_dir = "data-raw/",
  seed = 20232023     # 设置随机数种子，不要使用 set.seed() 函数
)

值得注意，这里，不需要设置参数初始值，但要设置 fixed_param = TRUE，表示根据模型生成模拟数据。

# 原始数据
simu_multi_normal$draws(variables = "yhat", format = "array")

# A draws_array: 1000 iterations, 1 chains, and 2 variables
, , variable = yhat[1,1]

         chain
iteration   1
        1 2.6
        2 5.3
        3 1.4
        4 3.1
        5 7.6

, , variable = yhat[1,2]

         chain
iteration    1
        1 0.65
        2 3.70
        3 4.36
        4 1.85
        5 2.32

# ... with 995 more iterations

# 数据概览
simu_multi_normal$summary(.num_args = list(sigfig = 4, notation = "dec"))

# A tibble: 2 × 10
  variable     mean  median      sd    mad      q5   q95  rhat ess_bulk ess_tail
  <chr>     <dec:4> <dec:4> <dec:4> <dec:> <dec:4> <dec> <dec>  <dec:4>  <dec:4>
1 yhat[1,1]   3.076   2.979   2.038 1.916  -0.3290 6.535 1.001   1140.    1023. 
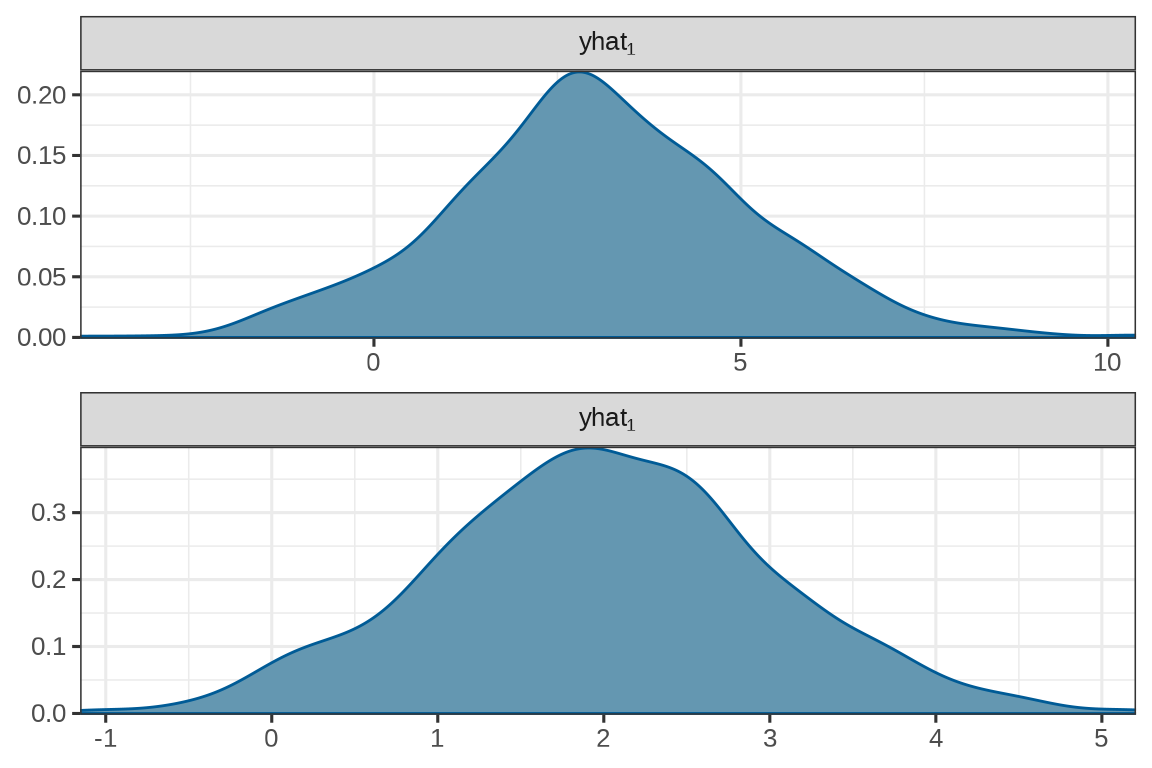
2 yhat[1,2]   1.990   1.964   1.018 0.9765  0.2323 3.680 1.002    966.5    982.1

以生成第一个服从二元正态分布的随机数（样本点）为例，这个随机数是通过采样获得的，采样过程中产生一个采样序列，采样序列的轨迹和分布如下：

library(ggplot2)
library(bayesplot)
mcmc_trace(simu_multi_normal$draws(c("yhat[1,1]", "yhat[1,2]")),
  facet_args = list(
    labeller = ggplot2::label_parsed,
    strip.position = "top", ncol = 1
  )
) + theme_bw(base_size = 12)

mcmc_dens(simu_multi_normal$draws(c("yhat[1,1]", "yhat[1,2]")),
  facet_args = list(
    labeller = ggplot2::label_parsed,
    strip.position = "top", ncol = 1
  )
) + theme_bw(base_size = 12)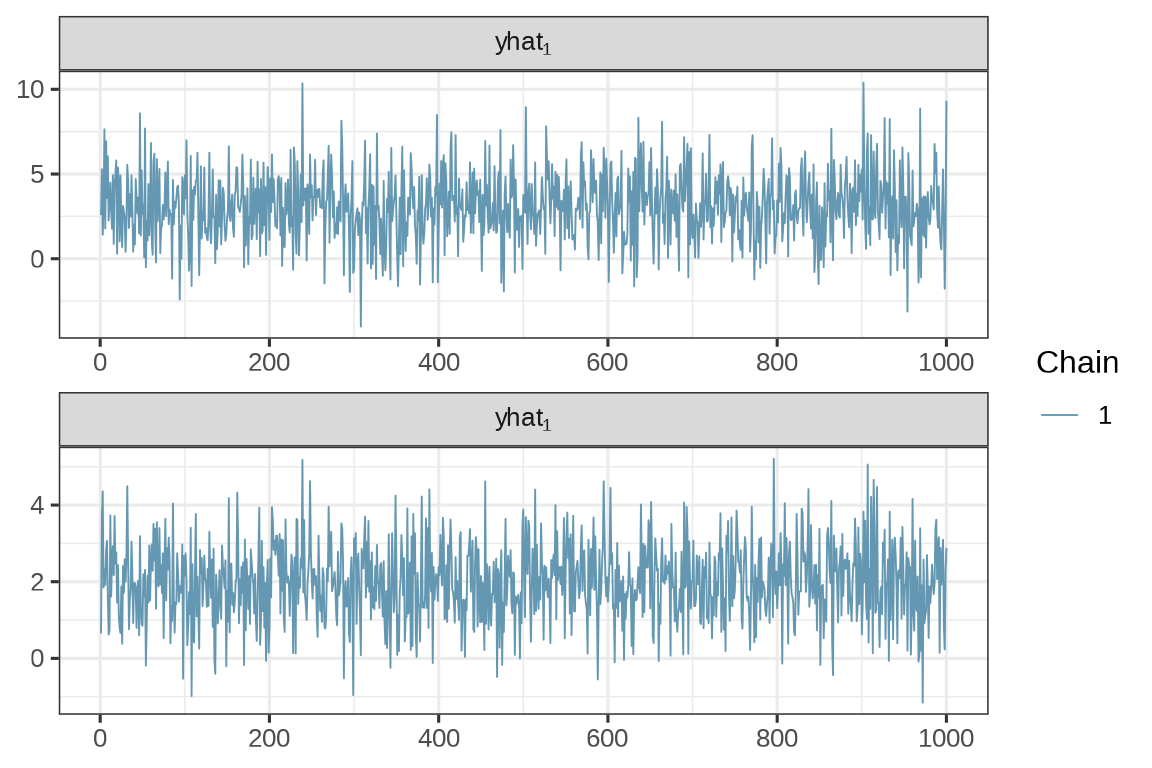

图 38.1: 采样序列的轨迹和分布

图 38.2: 采样序列的轨迹和分布

这就是一组来自二元正态分布的随机数。

mcmc_scatter(simu_multi_normal$draws(c("yhat[1,1]", "yhat[1,2]"))) +
  theme_bw(base_size = 12) +
  labs(x = expression(x[1]), y = expression(x[2]))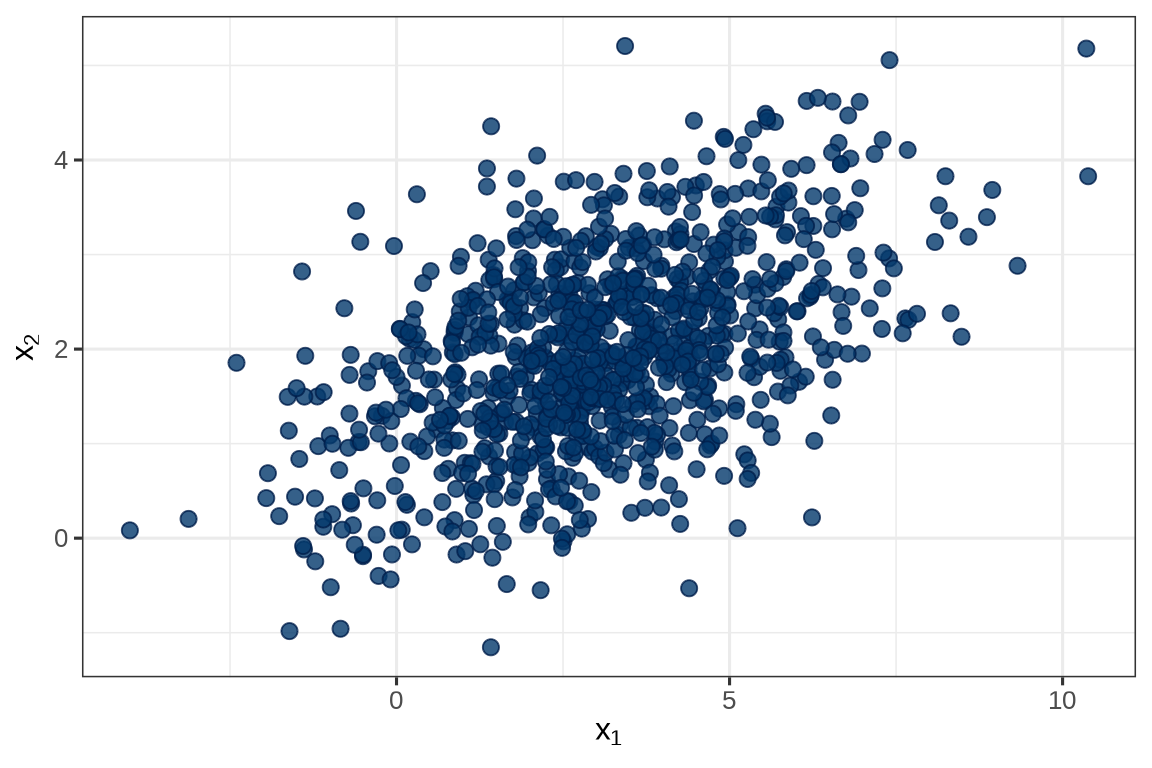

图 38.3: 生成二元正态分布的随机数

提取采样数据，整理成矩阵。

# 抽取原始采样数据
yhat <- simu_multi_normal$draws(c("yhat[1,1]", "yhat[1,2]"))
# 合并多条链
yhat_mean <- apply(yhat, c(1, 3), mean)
# 整理成二维矩阵
x <- as.matrix(yhat_mean)
# 样本均值
colMeans(x)

yhat[1,1] yhat[1,2] 
 3.076281  1.990465 

# 样本方差-协方差矩阵
var(x)

          yhat[1,1] yhat[1,2]
yhat[1,1]  4.152065  1.031544
yhat[1,2]  1.031544  1.035985

38.1.2 多元正态分布拟合

一般地，协方差矩阵的 Cholesky 分解的矩阵表示如下：

\[ \begin{aligned} \Sigma &= \begin{bmatrix} \sigma^2_1 & \rho_{12}\sigma_1\sigma_2 & \rho_{13}\sigma_1\sigma_3 \\ \rho_{12}\sigma_1\sigma_2 & \sigma_2^2 & \rho_{23}\sigma_2\sigma_3 \\ \rho_{13}\sigma_1\sigma_3 & \rho_{23}\sigma_2\sigma_3 & \sigma_3^2 \end{bmatrix} \\ & = \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix} \underbrace{ \begin{bmatrix} 1 & \rho_{12} & \rho_{13} \\ \rho_{12} & 1 & \rho_{23} \\ \rho_{13} & \rho_{23} & 1 \end{bmatrix} }_{R} \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix} \\ & = \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix} \underbrace{L_u L_u^{\top}}_{R} \begin{bmatrix} \sigma_1 & 0 & 0 \\ 0 & \sigma_2 & 0 \\ 0 & 0 & \sigma_3 \end{bmatrix} \end{aligned} \]

data {
  int<lower=1> N; // number of observations
  int<lower=1> K; // dimension of observations
  array[N] vector[K] y; // observations: a list of N vectors (each has K elements)
}
parameters {
  vector[K] mu;
  cholesky_factor_corr[K] Lcorr; // cholesky factor (L_u matrix for R)
  vector<lower=0>[K] sigma;
}
transformed parameters {
  corr_matrix[K] R; // correlation matrix
  cov_matrix[K] Sigma; // VCV matrix
  R = multiply_lower_tri_self_transpose(Lcorr); // R = Lcorr * Lcorr'
  Sigma = quad_form_diag(R, sigma); // quad_form_diag: diag_matrix(sig) * R * diag_matrix(sig)
}
model {
  sigma ~ cauchy(0, 5); // prior for sigma
  Lcorr ~ lkj_corr_cholesky(2.0); // prior for cholesky factor of a correlation matrix
  y ~ multi_normal(mu, Sigma);
}

代码中， 核心部分是关于多元正态分布的协方差矩阵的参数化，先将协方差矩阵中的方差和相关矩阵剥离，然后利用 Cholesky 分解将相关矩阵分解。在 Stan 里，这是一套高效的组合。

• 类型 cholesky_factor_corr 表示相关矩阵的 Cholesky 分解后的矩阵 \(L_u\)

• 类型 corr_matrix 表示相关矩阵 \(R\) 。

• 类型 cov_matrix 表示协方差矩阵 \(\Sigma\) 。

• 函数 lkj_corr_cholesky 为相关矩阵 Cholesky 分解后的矩阵 \(L_u\) 服从的分布，详见 Cholesky LKJ correlation distribution。函数名中的 lkj 是以三个人的人名的首字母命名的 Lewandowski, Kurowicka, and Joe 2009。

• 函数 multiply_lower_tri_self_transpose 为下三角矩阵与它的转置的乘积，详见 Correlation Matrix Distributions。

• 函数 multi_normal 为多元正态分布的抽样语句，详见 Multivariate normal distribution。

矩阵 \(L_u\) 是相关矩阵 \(R\) 的 Cholesky 分解的结果，在贝叶斯框架内，参数都是随机的，相关矩阵是一个随机矩阵，矩阵 \(L_u\) 是一个随机矩阵，它的分布用 Stan 代码表示为如下：

L ~ lkj_corr_cholesky(2.0); # implies L * L' ~ lkj_corr(2.0);

LKJ 分布有一个参数 \(\eta\) ，此处 \(\eta = 2\) ，意味着变量之间的相关性较弱，LKJ 分布的概率密度函数正比于相关矩阵的行列式的 \(\eta-1\) 次幂 \((\det{R})^{\eta-1}\)，LKJ 分布的详细说明见Lewandowski-Kurowicka-Joe (LKJ) distribution。

有了上面的背景知识，下面先在 R 环境中模拟一组来自多元正态分布的样本。

set.seed(20232023)
# 均值
mu <- c(1, 2, -5) 
# 相关矩阵 (R)
R <- matrix(c(
  1, 0.7, 0.2, 
  0.7, 1, -0.5,
  0.2, -0.5, 1
), 3)
# sd1 = 0.5, sd2 = 1.2, sd3 = 2.3
sigmas <- c(0.5, 1.2, 2.3) 
# 方差-协方差矩阵
Sigma <- diag(sigmas) %*% R %*% diag(sigmas) 
# 模拟 1000 个样本数据
dat <- MASS::mvrnorm(1000, mu = mu, Sigma = Sigma) 

根据 1000 个样本点，估计多元正态分布的均值参数和方差协方差参数。

# 来自多元正态分布的一组观测数据
multi_normal_chol_d <- list(
  N = 1000, # 样本量
  K = 3,    # 三维
  y = dat
)
# 编译多元正态分布模型
mod_multi_normal_chol <- cmdstan_model(
  stan_file = "code/multi_normal_fitted.stan",
  compile = TRUE, cpp_options = list(stan_threads = TRUE)
)
# 拟合多元正态分布模型
fit_multi_normal <- mod_multi_normal_chol$sample(
  data = multi_normal_chol_d,
  iter_warmup = 500,    # 每条链预处理迭代次数
  iter_sampling = 1000, # 每条链采样次数
  chains = 2,           # 马尔科夫链的数目
  parallel_chains = 1,  # 指定 CPU 核心数
  threads_per_chain = 1,  # 每条链设置一个线程
  show_messages = FALSE,  # 不显示迭代的中间过程
  refresh = 0,            # 不显示采样的进度
  output_dir = "data-raw/",
  seed = 20232023     # 设置随机数种子
)

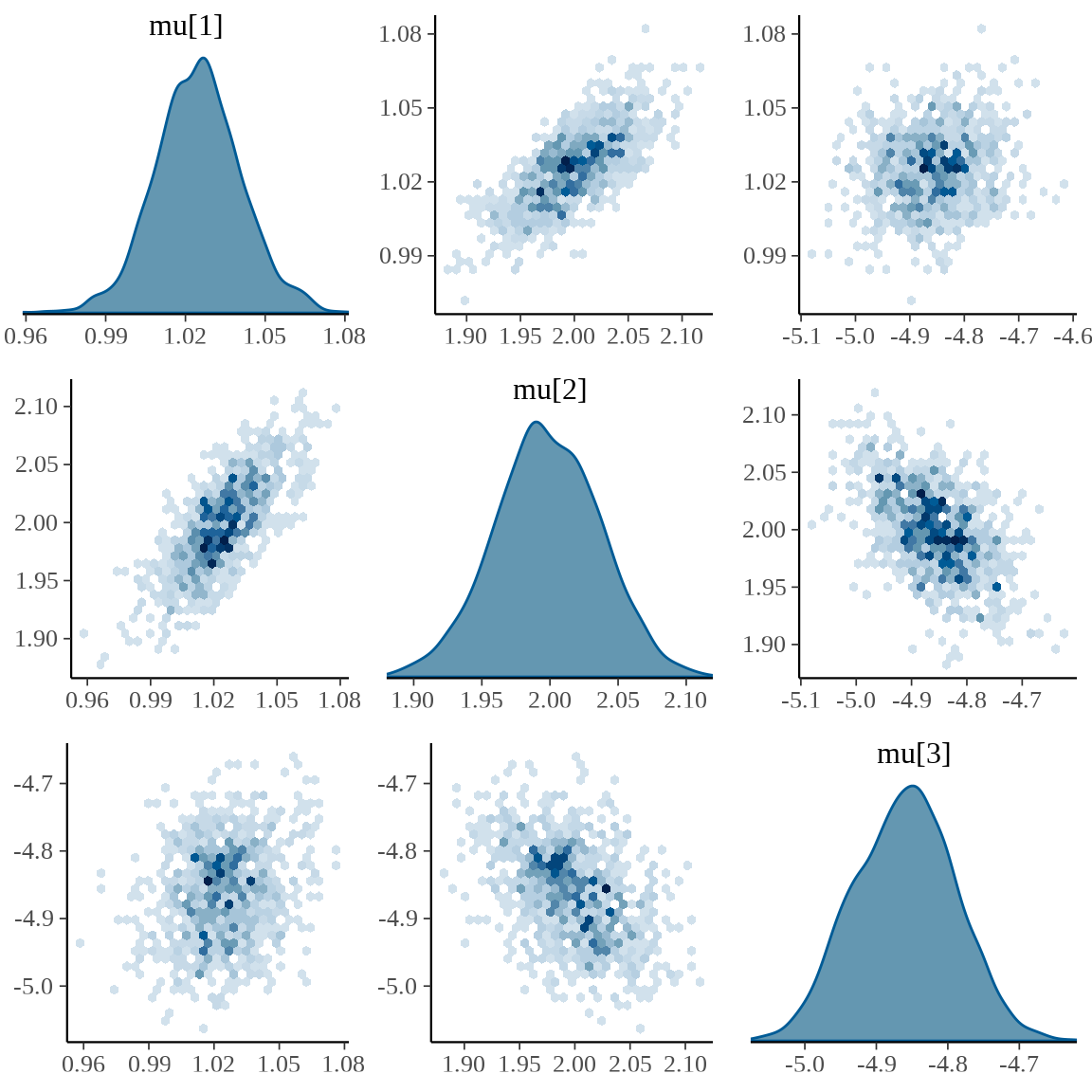
均值向量 \(\bm{\mu}\) 和协方差矩阵 \(\Sigma\) 估计结果如下：

fit_multi_normal$summary(c("mu", "Sigma"), .num_args = list(sigfig = 3, notation = "dec"))

# A tibble: 12 × 10
   variable      mean median     sd    mad     q5    q95  rhat ess_bulk ess_tail
   <chr>      <dec:3> <dec:> <dec:> <dec:> <dec:> <dec:> <dec>  <dec:3>  <dec:3>
 1 mu[1]        1.02   1.02  0.0162 0.0154  0.999  1.05   1.00    1605.    1250.
 2 mu[2]        2.00   2.00  0.0385 0.0386  1.93   2.06   1.00    1300.    1138.
 3 mu[3]       -4.86  -4.86  0.0703 0.0724 -4.98  -4.75   1.00    1737.    1549.
 4 Sigma[1,1]   0.250  0.249 0.0110 0.0108  0.231  0.268  1.00    1847.    1336.
 5 Sigma[2,1]   0.427  0.426 0.0235 0.0234  0.388  0.466  1.00    1507.    1261.
 6 Sigma[3,1]   0.210  0.209 0.0361 0.0363  0.151  0.271  1.00    1472.    1202.
 7 Sigma[1,2]   0.427  0.426 0.0235 0.0234  0.388  0.466  1.00    1507.    1261.
 8 Sigma[2,2]   1.47   1.47  0.0649 0.0635  1.37   1.58   1.01    1506.    1265.
 9 Sigma[3,2]  -1.41  -1.41  0.0955 0.0957 -1.57  -1.26   1.00    1643.    1572.
10 Sigma[1,3]   0.210  0.209 0.0361 0.0363  0.151  0.271  1.00    1472.    1202.
11 Sigma[2,3]  -1.41  -1.41  0.0955 0.0957 -1.57  -1.26   1.00    1643.    1572.
12 Sigma[3,3]   5.28   5.27  0.225  0.221   4.92   5.67   1.00    1605.    1603.

均值向量 \(\bm{\mu} = (\mu_1,\mu_2,\mu_3)^{\top}\) 各个分量及其两两相关性，如下图所示。

mcmc_pairs(
  fit_multi_normal$draws(c("mu[1]", "mu[2]", "mu[3]")),
  diag_fun = "dens", off_diag_fun = "hex"
)

图 38.4: 三元正态分布

38.2 二维高斯过程

高斯过程定义

38.2.1 二维高斯过程模拟

二维高斯过程 \(\mathcal{S}\) 的均值向量为 0 向量，自协方差函数为指数型，如下

\[ \mathsf{Cov}\{S(x_i), S(x_j)\} = \sigma^2 \exp\big( -\frac{\|x_i -x_j\|_{2}}{\phi} \big) \]

其中，不妨设参数 \(\sigma = 10, \phi = 1\) 。模拟高斯过程的 Stan 代码如下

data {
  int<lower=1> N;
  int<lower=1> D;
  array[N] vector[D] X;
  vector[N] mu;
  real<lower=0> sigma;
  real<lower=0> phi;
}
transformed data {
  real delta = 1e-9;
  matrix[N, N] L;
  matrix[N, N] K = gp_exponential_cov(X, sigma, phi) + diag_matrix(rep_vector(delta, N));
  L = cholesky_decompose(K);
}
parameters {
  vector[N] eta;
}
model {
  eta ~ std_normal();
}
generated quantities {
  vector[N] y;
  y = mu + L * eta;
}

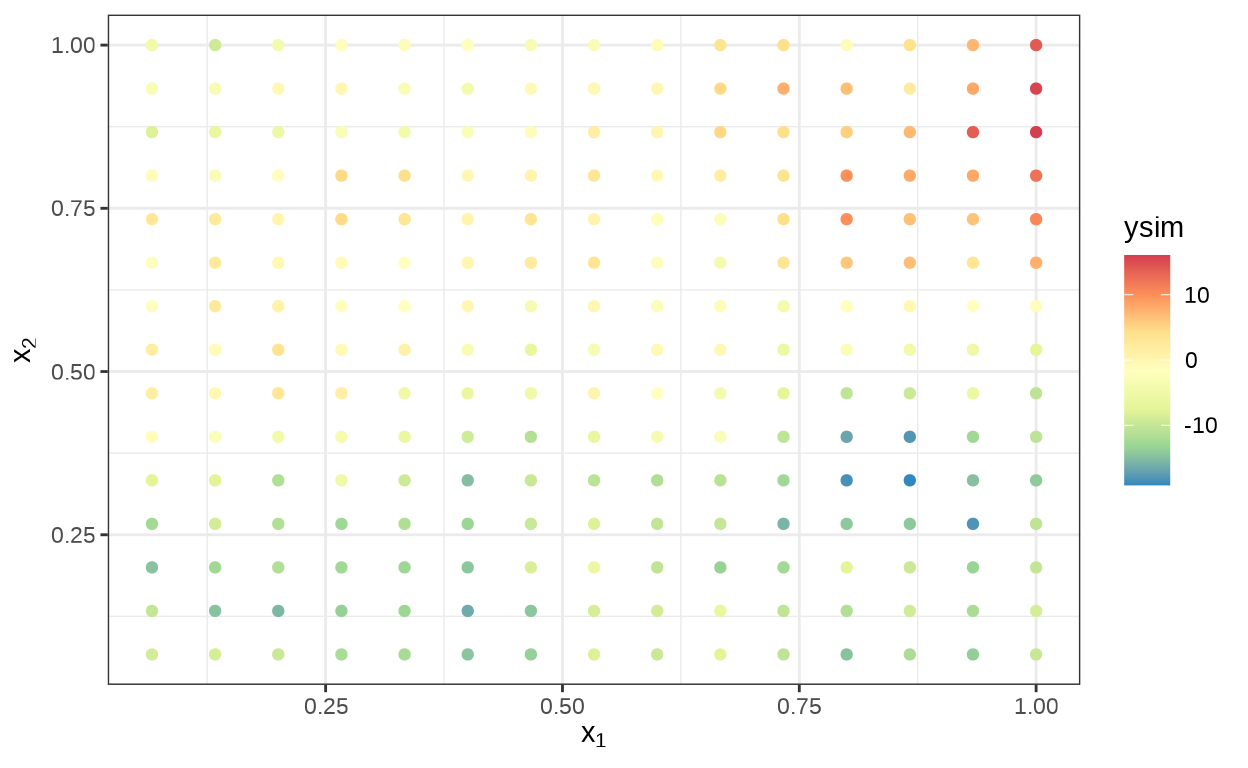
在二维规则网格上采样，采样点数量为 225。

n <- 15
gaussian_process_d <- list(
  N = n^2,
  D = 2,
  mu = rep(0, n^2),
  sigma = 10,
  phi = 1,
  X = expand.grid(x1 = 1:n / n, x2 = 1:n / n)
)
# 编译二维高斯过程模型
mod_gaussian_process_simu <- cmdstan_model(
  stan_file = "code/gaussian_process_simu.stan",
  compile = TRUE, cpp_options = list(stan_threads = TRUE)
)

模拟 1 个样本，因为是模拟数据，不需要设置多条链。

fit_multi_normal_gp <- mod_gaussian_process_simu$sample(
  data = gaussian_process_d,
  iter_warmup = 500,       # 每条链预处理迭代次数
  iter_sampling = 1000,    # 样本量
  chains = 1,              # 马尔科夫链的数目
  parallel_chains = 1,    # 指定 CPU 核心数
  threads_per_chain = 1,  # 每条链设置一个线程
  show_messages = FALSE,  # 不显示迭代的中间过程
  refresh = 0,            # 不显示采样的进度
  output_dir = "data-raw/",
  seed = 20232023         # 设置随机数种子
)

位置 1 和 2 处的随机变量的迭代轨迹，均值为 0 ，标准差 10 左右。

mcmc_trace(fit_multi_normal_gp$draws(c("y[1]", "y[2]")),
  facet_args = list(
    labeller = ggplot2::label_parsed,
    strip.position = "top", ncol = 1
  )
) + theme_bw(base_size = 12)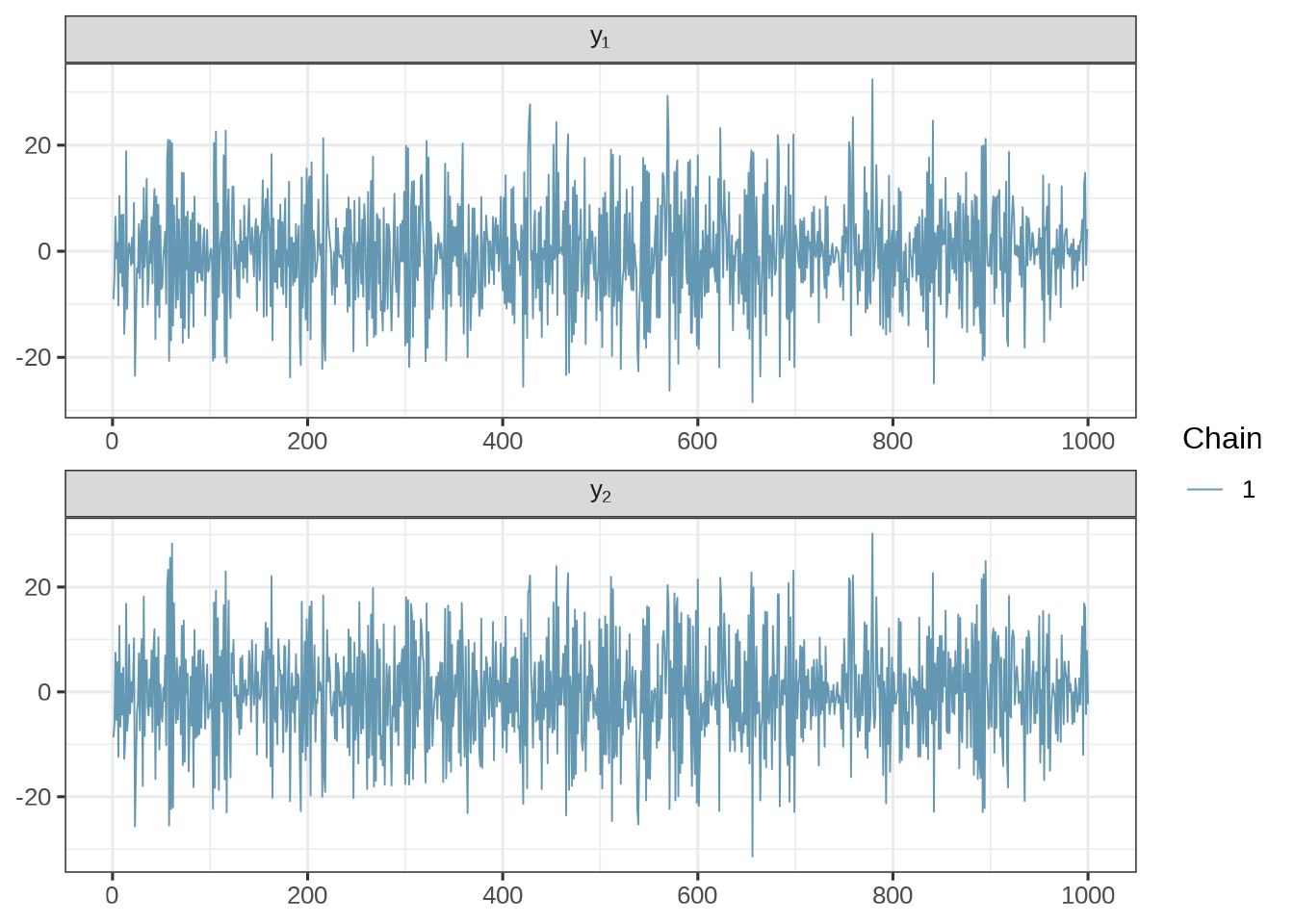

图 38.5: 位置 1 和 2 处的迭代轨迹

位置 1 处的随机变量及其分布

y1 <- fit_multi_normal_gp$draws(c("y[1]"), format = "draws_array")
# 合并链条结果
y1_mean <- apply(y1, c(1, 3), mean)
# y[1] 的方差
var(y1_mean)

         y[1]
y[1] 100.5436

# y[1] 的标准差
sd(y1_mean)

[1] 10.02714

100 次迭代获得 100 个样本点，每次迭代采集一个样本点，每个样本点是一个 225 维的向量。

# 抽取原始的采样数据
y_array <- fit_multi_normal_gp$draws(variables = "y", format = "array")
# 合并链条
y_mean <- apply(y_array, c(1, 3), mean)

从 100 次迭代中任意提取某一个样本点，比如预采样之后的第一次下迭代的结果，接着整理数据。

# 整理数据
sim_gp_data <- cbind.data.frame(gaussian_process_d$X, ysim = y_mean[1, ])

绘制二维高斯过程图形。

ggplot(data = sim_gp_data, aes(x = x1, y = x2)) +
  geom_point(aes(color = ysim)) +
  scale_color_distiller(palette = "Spectral") +
  theme_bw() +
  labs(x = expression(x[1]), y = expression(x[2]))

图 38.6: 二维高斯过程

38.2.2 二维高斯过程拟合

二维高斯过程拟合代码如下

data {
  int<lower=1> N;
  int<lower=1> D;
  array[N] vector[D] x;
  vector[N] y;
}
transformed data {
  real delta = 1e-9;
  vector[N] mu = rep_vector(0, N);
}
parameters {
  real<lower=0> phi;
  real<lower=0> sigma;
}
model {
  matrix[N, N] L_K;
  {
    matrix[N, N] K = gp_exponential_cov(x, sigma, phi) + diag_matrix(rep_vector(delta, N));
    L_K = cholesky_decompose(K);
  }
  
  phi ~ std_normal();
  sigma ~ std_normal();

  y ~ multi_normal_cholesky(mu, L_K);
}

# 二维高斯过程模型
gaussian_process_d <- list(
  D = 2,
  N = nrow(sim_gp_data), # 观测记录的条数
  x = sim_gp_data[, c("x1", "x2")],
  y = sim_gp_data[, "ysim"]
)

nchains <- 2
set.seed(20232023)
# 给每条链设置不同的参数初始值
inits_gaussian_process <- lapply(1:nchains, function(i) {
  list(
    sigma = runif(1),
    phi = runif(1)
  )
})

# 编译模型
mod_gaussian_process <- cmdstan_model(
  stan_file = "code/gaussian_process_fitted.stan",
  compile = TRUE, cpp_options = list(stan_threads = TRUE)
)

# 拟合二维高斯过程
fit_gaussian_process <- mod_gaussian_process$sample(
  data = gaussian_process_d,     # 观测数据
  init = inits_gaussian_process, # 迭代初值
  iter_warmup = 1000,   # 每条链预处理迭代次数
  iter_sampling = 2000, # 每条链总迭代次数
  chains = nchains,     # 马尔科夫链的数目
  parallel_chains = 2,  # 指定 CPU 核心数，可以给每条链分配一个
  threads_per_chain = 2, # 每条链设置一个线程
  show_messages = FALSE, # 不显示迭代的中间过程
  refresh = 0,           # 不显示采样的进度
  output_dir = "data-raw/",
  seed = 20232023        # 设置随机数种子，不要使用 set.seed() 函数
)
# 诊断
fit_gaussian_process$diagnostic_summary()

$num_divergent
[1] 0 0

$num_max_treedepth
[1] 0 0

$ebfmi
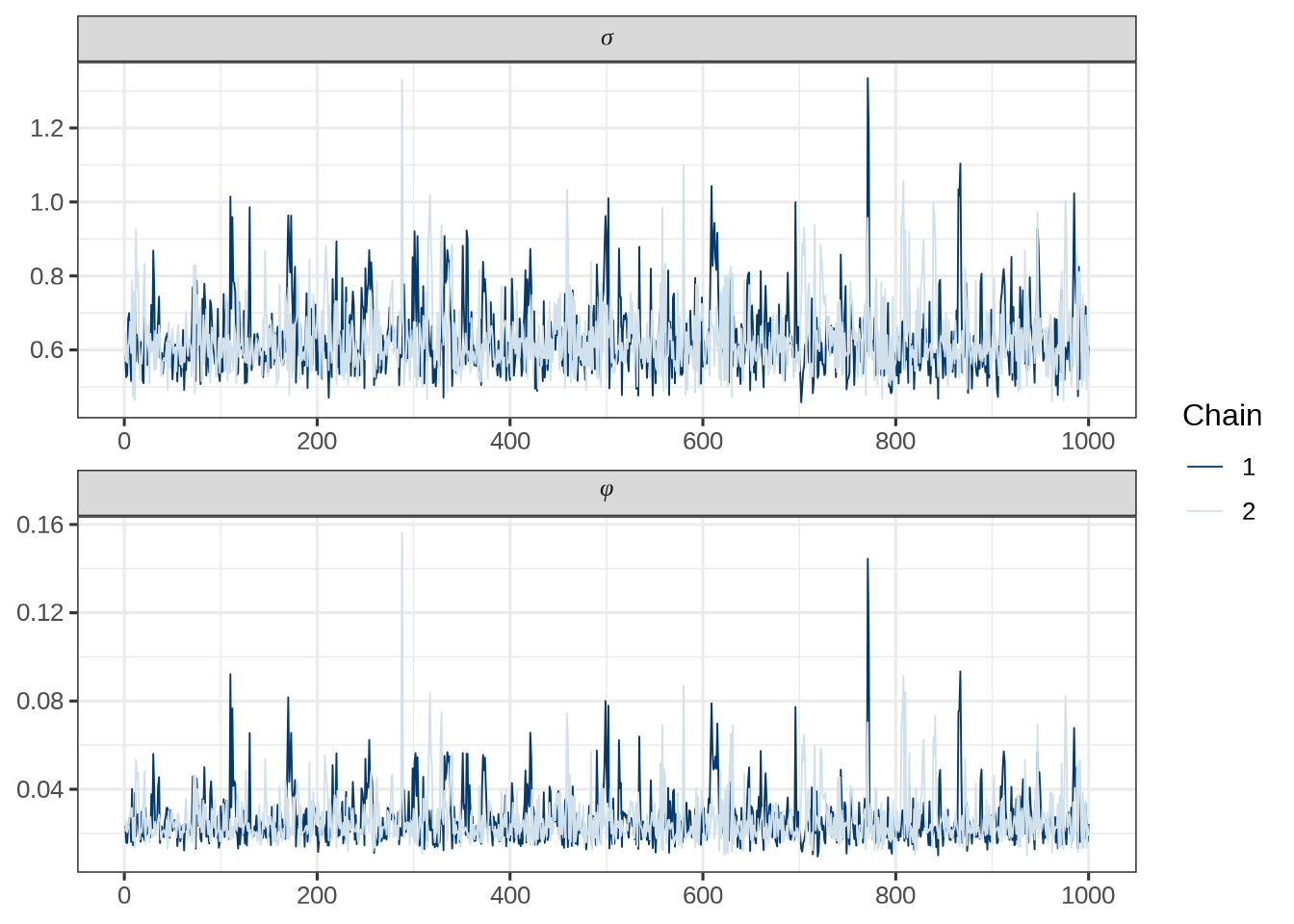
[1] 1.097944 1.083674

输出结果

fit_gaussian_process$summary()

# A tibble: 3 × 10
  variable     mean   median     sd    mad       q5      q95  rhat ess_bulk
  <chr>       <num>    <num>  <num>  <num>    <num>    <num> <num>    <num>
1 lp__     -354.    -354.    0.964  0.703  -356.    -353.     1.00    1395.
2 phi         0.308    0.302 0.0503 0.0486    0.235    0.400  1.00    1196.
3 sigma       5.25     5.24  0.389  0.375     4.65     5.94   1.00    1246.
# ℹ 1 more variable: ess_tail <num>

38.3 高斯过程回归

38.3.1 模型介绍

朗格拉普岛是位于太平洋上的一个小岛，因美国在比基尼群岛的氢弹核试验受到严重的核辐射影响，数十年之后，科学家登岛采集核辐射强度数据以评估当地居民重返该岛的可能性。朗格拉普岛是一个十分狭长且占地面积只有几平方公里的小岛。

根据 \({}^{137}\mathrm{Cs}\) 放出伽马射线，在 \(n=157\) 个采样点，分别以时间间隔 \(t_i\) 测量辐射量 \(y(x_i)\)，建立泊松型空间广义线性混合效应模型(Diggle, Tawn, 和 Moyeed 1998)。

\[ \begin{aligned} \log\{\lambda(x_i)\} & = \beta + S(x_{i})\\ y(x_{i}) &\sim \mathrm{Poisson}\big(t_i\lambda(x_i)\big) \end{aligned} \]

其中，\(\beta\) 表示截距，相当于平均水平，\(\lambda(x_i)\) 表示位置 \(x_i\) 处的辐射强度，\(S(x_{i})\) 表示位置 \(x_i\) 处的空间效应，\(S(x),x \in \mathcal{D} \subset{\mathbb{R}^2}\) 是二维平稳空间高斯过程 \(\mathcal{S}\) 的具体实现。 \(\mathcal{D}\) 表示研究区域，可以理解为朗格拉普岛，它是二维实平面 \(\mathbb{R}^2\) 的子集。

随机过程 \(S(x)\) 的自协方差函数常用的有指数型、幂二次指数型（高斯型）和梅隆型，形式如下：

\[ \begin{aligned} \mathsf{Cov}\{S(x_i), S(x_j)\} &= \sigma^2 \exp\big( -\frac{\|x_i -x_j\|_{2}}{\phi} \big) \\ \mathsf{Cov}\{ S(x_i), S(x_j) \} &= \sigma^2 \exp\big( -\frac{\|x_i -x_j\|_{2}^{2}}{2\phi^2} \big) \\ \mathsf{Cov}\{ S(x_i), S(x_j) \} &= \sigma^2 \frac{2^{1 - \nu}}{\Gamma(\nu)} \left(\sqrt{2\nu}\frac{\|x_i -x_j\|_{2}}{\phi}\right)^{\nu} K_{\nu}\left(\sqrt{2\nu}\frac{\|x_i -x_j\|_{2}}{\phi}\right) \\ K_{\nu}(x) &= \int_{0}^{\infty}\exp(-x \cosh t) \cosh (\nu t) \mathrm{dt} \end{aligned} \]

待估参数：代表方差的 \(\sigma^2\) 和代表范围的 \(\phi\) 。当 \(\nu = 1/2\) 时，梅隆型退化为指数型。

38.3.2 观测数据

# 加载数据
rongelap <- readRDS(file = "data/rongelap.rds")
rongelap_coastline <- readRDS(file = "data/rongelap_coastline.rds")
# 准备输入数据
rongelap_poisson_d <- list(
  N = nrow(rongelap), # 观测记录的条数
  D = 2, # 2 维坐标
  X = rongelap[, c("cX", "cY")] / 6000, # N x 2 矩阵
  y = rongelap$counts, # 响应变量
  offsets = rongelap$time # 漂移项
)
# 准备参数初始化数据
set.seed(20232023)
nchains <- 2 # 2 条迭代链
inits_data_poisson <- lapply(1:nchains, function(i) {
  list(
    beta = rnorm(1),
    sigma = runif(1),
    phi = runif(1),
    lambda = rnorm(157)
  )
})

38.3.3 预测数据

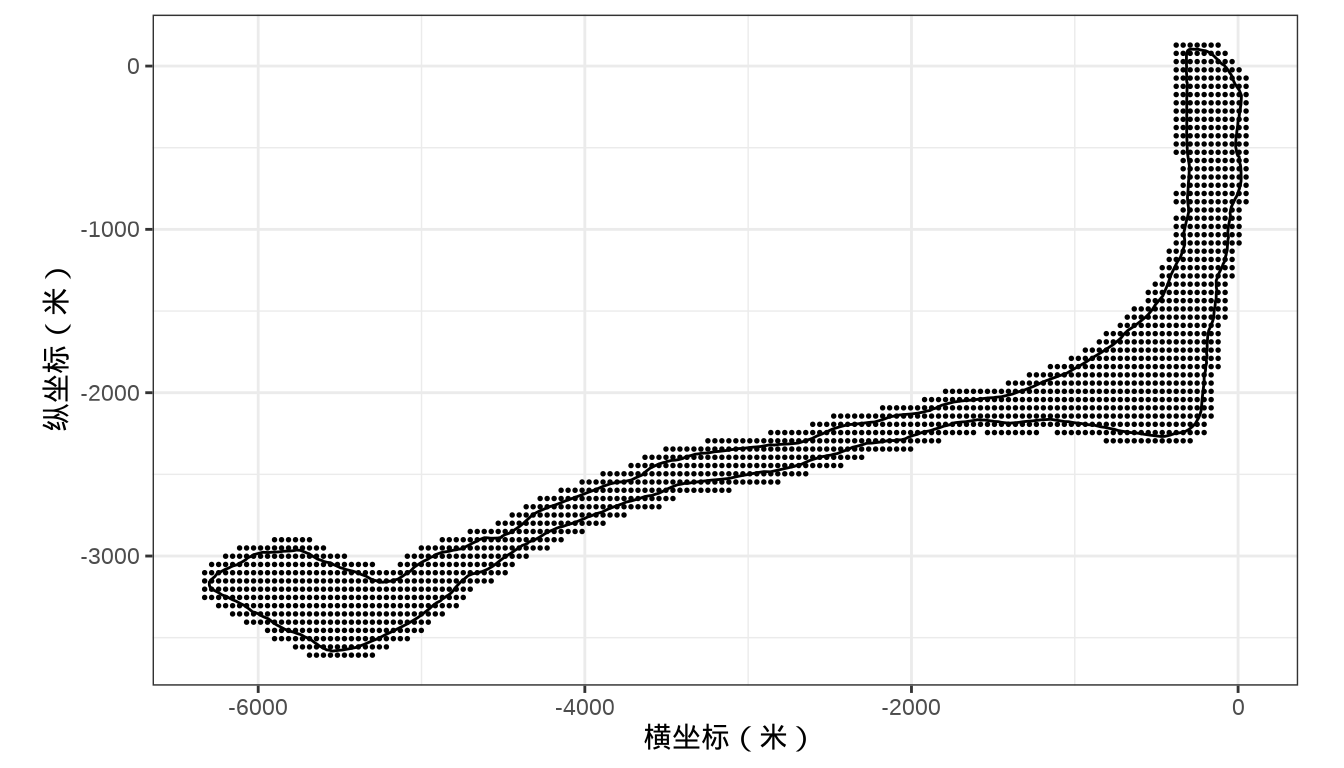
预测未采样的位置的核辐射强度，根据海岸线数据网格化全岛，以格点代表未采样的位置

library(sf)
library(abind)
library(stars)
# 类型转化
rongelap_sf <- st_as_sf(rongelap, coords = c("cX", "cY"), dim = "XY")
rongelap_coastline_sf <- st_as_sf(rongelap_coastline, coords = c("cX", "cY"), dim = "XY")
rongelap_coastline_sfp <- st_cast(st_combine(st_geometry(rongelap_coastline_sf)), "POLYGON")
# 添加缓冲区
rongelap_coastline_buffer <- st_buffer(rongelap_coastline_sfp, dist = 50)
# 构造带边界约束的网格
rongelap_coastline_grid <- st_make_grid(rongelap_coastline_buffer, n = c(150, 75))
# 将 sfc 类型转化为 sf 类型
rongelap_coastline_grid <- st_as_sf(rongelap_coastline_grid)
rongelap_coastline_buffer <- st_as_sf(rongelap_coastline_buffer)
rongelap_grid <- rongelap_coastline_grid[rongelap_coastline_buffer, op = st_intersects]
# 计算网格中心点坐标
rongelap_grid_centroid <- st_centroid(rongelap_grid)
# 共计 1612 个预测点
rongelap_grid_df <- as.data.frame(st_coordinates(rongelap_grid_centroid))
colnames(rongelap_grid_df) <- c("cX", "cY")

未采样的位置 rongelap_grid_df

head(rongelap_grid_df)

         cX        cY
1 -5685.942 -3606.997
2 -5643.145 -3606.997
3 -5600.347 -3606.997
4 -5557.549 -3606.997
5 -5514.751 -3606.997
6 -5471.953 -3606.997

朗格拉普岛网格化生成格点

ggplot() +
  geom_point(data = rongelap_grid_df, aes(x = cX, y = cY), cex = 0.3) +
  geom_path(data = rongelap_coastline, aes(x = cX, y = cY)) +
  coord_fixed() +
  theme_bw() +
  labs(x = "横坐标（米）", y = "纵坐标（米）")

图 38.7: 朗格拉普岛

38.3.4 模型编码

指定各个参数 \(\beta,\sigma,\phi\) 的先验分布

\[ \begin{aligned} \beta &\sim \mathrm{std\_normal}(0,1) \\ \sigma &\sim \mathrm{inv\_gamma}(5,5) \\ \phi &\sim \mathrm{half\_std\_normal}(0,1) \\ \bm{\lambda} | \beta,\sigma &\sim \mathrm{multivariate\_normal}(\bm{\beta}, \sigma^2 \Sigma) \\ \bm{y} | \bm{\lambda} &\sim \mathrm{poisson\_log}\big(\log(\text{offsets})+\bm{\lambda}\big) \end{aligned} \]

其中，\(\beta,\sigma,\phi,\Sigma\) 的含义同前，\(\lambda\) 代表辐射强度，\(\mathrm{offsets}\) 代表漂移项，这里是时间段，\(\bm{y}\) 表示观测的辐射粒子数，\(\mathrm{poisson\_log}\) 表示泊松分布的对数参数化，将频率参数 rate 的对数 \(\lambda\) 作为参数，详见 Stan 函数手册中泊松分布的对数函数表示。

data {
  int<lower=1> N;
  int<lower=1> D;
  array[N] vector[D] X;
  array[N] int<lower = 0> y;
  vector[N] offsets;
}
transformed data {
  real delta = 1e-12;
  vector[N] log_offsets = log(offsets);
}
parameters {
  real beta;
  real<lower=0> sigma;
  real<lower=0> phi;
  vector[N] lambda;
}
transformed parameters {
  vector[N] mu = rep_vector(beta, N);
}
model {
  matrix[N, N] L_K;
  {
    matrix[N, N] K = gp_exponential_cov(X, sigma, phi) + diag_matrix(rep_vector(delta, N));
    L_K = cholesky_decompose(K);
  }
  
  beta ~ std_normal();
  sigma ~ inv_gamma(5, 5);
  phi ~ std_normal();
  
  lambda ~ multi_normal_cholesky(mu, L_K);
  y ~ poisson_log(log_offsets + lambda);
}

# 编译模型
mod_rongelap_poisson <- cmdstan_model(
  stan_file = "code/rongelap_poisson_processes.stan",
  compile = TRUE, cpp_options = list(stan_threads = TRUE)
)
# 泊松对数模型
fit_rongelap_poisson <- mod_rongelap_poisson$sample(
  data = rongelap_poisson_d,  # 观测数据
  init = inits_data_poisson,  # 迭代初值
  iter_warmup = 500,    # 每条链预处理迭代次数
  iter_sampling = 1000, # 每条链总迭代次数
  chains = nchains,     # 马尔科夫链的数目
  parallel_chains = 2,  # 指定 CPU 核心数，可以给每条链分配一个
  threads_per_chain = 2, # 每条链设置一个线程
  show_messages = FALSE, # 不显示迭代的中间过程
  refresh = 0,           # 不显示采样的进度
  output_dir = "data-raw/",
  seed = 20232023
)
# 诊断
fit_rongelap_poisson$diagnostic_summary()

$num_divergent
[1] 0 0

$num_max_treedepth
[1] 0 0

$ebfmi
[1] 0.9629484 1.1461127

# 泊松对数模型
fit_rongelap_poisson$summary(
  variables = c("lp__", "beta", "sigma", "phi"),
  .num_args = list(sigfig = 3, notation = "dec")
)

# A tibble: 4 × 10
  variable         mean       median      sd      mad           q5          q95
  <chr>         <dec:3>      <dec:3> <dec:3>  <dec:3>      <dec:3>      <dec:3>
1 lp__     3402193.     3402190       9.42   14.8     3402180      3402210     
2 beta           1.78         1.79    0.140   0.119         1.54         1.98  
3 sigma          0.632        0.613   0.100   0.0792        0.512        0.819 
4 phi            0.0265       0.0233  0.0123  0.00799       0.0142       0.0500
# ℹ 3 more variables: rhat <dec:3>, ess_bulk <dec:3>, ess_tail <dec:3>

# 参数的迭代轨迹
mcmc_trace(fit_rongelap_poisson$draws(c("sigma", "phi")),
           facet_args = list(
             labeller = ggplot2::label_parsed,
             strip.position = "top", ncol = 1
           )
) + theme_bw(base_size = 12)

图 38.8: \(\sigma\) 和 \(\phi\) 的迭代轨迹

# 参数的后验分布
mcmc_dens(fit_rongelap_poisson$draws(c("sigma", "phi")),
          facet_args = list(
            labeller = ggplot2::label_parsed,
            strip.position = "top", ncol = 1
          )
) + theme_bw(base_size = 12)

图 38.9: \(\sigma\) 和 \(\phi\) 的后验分布

38.3.5 预测分布

核辐射预测模型的 Stan 代码

functions {
  vector gp_pred_rng(array[] vector x2,
                     vector lambda,
                     array[] vector x1,
                     real beta,
                     real sigma,
                     real phi,
                     real delta) {
    int N1 = rows(lambda);
    int N2 = size(x2);
    vector[N2] f2;
    {
      matrix[N1, N1] L_K;
      vector[N1] K_div_lambda;
      matrix[N1, N2] k_x1_x2;
      matrix[N1, N2] v_pred;
      vector[N2] f2_mu;
      matrix[N2, N2] cov_f2;
      matrix[N2, N2] diag_delta;
      matrix[N1, N1] K;
      K = gp_exponential_cov(x1, sigma, phi);
      L_K = cholesky_decompose(K);
      K_div_lambda = mdivide_left_tri_low(L_K, lambda - beta);
      K_div_lambda = mdivide_right_tri_low(K_div_lambda', L_K)';
      k_x1_x2 = gp_exponential_cov(x1, x2, sigma, phi);
      f2_mu = beta + (k_x1_x2' * K_div_lambda);
      v_pred = mdivide_left_tri_low(L_K, k_x1_x2);
      cov_f2 = gp_exponential_cov(x2, sigma, phi) - v_pred' * v_pred;
      diag_delta = diag_matrix(rep_vector(delta, N2));

      f2 = multi_normal_rng(f2_mu, cov_f2 + diag_delta);
    }
    return f2;
  }
}
data {
  int<lower=1> D;
  int<lower=1> N1;
  array[N1] vector[D] x1;
  array[N1] int<lower = 0> y1;
  vector[N1] offsets1;
  int<lower=1> N2;
  array[N2] vector[D] x2;
  vector[N2] offsets2;
}
transformed data {
  real delta = 1e-12;
  vector[N1] log_offsets1 = log(offsets1);
  vector[N2] log_offsets2 = log(offsets2);
  
  int<lower=1> N = N1 + N2;
  array[N] vector[D] x;
  
  for (n1 in 1:N1) {
    x[n1] = x1[n1];
  }
  for (n2 in 1:N2) {
    x[N1 + n2] = x2[n2];
  }
}
parameters {
  real beta;
  real<lower=0> sigma;
  real<lower=0> phi;
  vector[N1] lambda1;
}
transformed parameters {
  vector[N1] mu = rep_vector(beta, N1);
}
model {
  matrix[N1, N1] L_K;
  {
    matrix[N1, N1] K = gp_exponential_cov(x1, sigma, phi) + diag_matrix(rep_vector(delta, N1));
    L_K = cholesky_decompose(K);
  }

  beta ~ std_normal();
  sigma ~ inv_gamma(5, 5);
  phi ~ std_normal();
  
  lambda1 ~ multi_normal_cholesky(mu, L_K);
  y1 ~ poisson_log(log_offsets1 + lambda1);
}
generated quantities {
  vector[N1] yhat;     // Posterior predictions for each location
  vector[N1] log_lik;  // Log likelihood for each location
  vector[N1] RR1 = log_offsets1 + lambda1;
  
  for(n in 1:N1) {
    log_lik[n] = poisson_log_lpmf(y1[n] | RR1[n]);
    yhat[n] = poisson_log_rng(RR1[n]);
  }
  
  vector[N2] ypred; 
  vector[N2] lambda2 = gp_pred_rng(x2, lambda1, x1, beta, sigma, phi, delta);
  vector[N2] RR2 = log_offsets2 + lambda2;
  
  for(n in 1:N2) {
    ypred[n] = poisson_log_rng(RR2[n]);
  }
}

准备数据、拟合模型

# 固定漂移项
rongelap_grid_df$time <- 100
# 对数高斯模型
rongelap_poisson_pred_d <- list(
  D = 2,
  N1 = nrow(rongelap), # 观测记录的条数
  x1 = rongelap[, c("cX", "cY")] / 6000,
  y1 = rongelap[, "counts"],
  offsets1 = rongelap[, "time"],
  N2 = nrow(rongelap_grid_df), # 2 维坐标
  x2 = rongelap_grid_df[, c("cX", "cY")] / 6000,
  offsets2 = rongelap_grid_df[, "time"]
)
# 迭代链数目
nchains <- 2
# 给每条链设置不同的参数初始值
inits_data_poisson_pred <- lapply(1:nchains, function(i) {
  list(
    beta = rnorm(1),
    sigma = runif(1),
    phi = runif(1),
    lambda = rnorm(157)
  )
})
# 编译模型
mod_rongelap_poisson_pred <- cmdstan_model(
  stan_file = "code/rongelap_poisson_pred.stan",
  compile = TRUE, cpp_options = list(stan_threads = TRUE)
)
# 泊松模型
fit_rongelap_poisson_pred <- mod_rongelap_poisson_pred$sample(
  data = rongelap_poisson_pred_d,   # 观测数据
  init = inits_data_poisson_pred,   # 迭代初值
  iter_warmup = 500,            # 每条链预处理迭代次数
  iter_sampling = 1000,         # 每条链总迭代次数
  chains = nchains,             # 马尔科夫链的数目
  parallel_chains = 2,      # 指定 CPU 核心数，可以给每条链分配一个
  threads_per_chain = 2,    # 每条链设置一个线程
  show_messages = FALSE,    # 不显示迭代的中间过程
  refresh = 0,              # 不显示采样的进度
  output_dir = "data-raw/",
  seed = 20232023           # 设置随机数种子，不要使用 set.seed() 函数
)
# 诊断信息
fit_rongelap_poisson_pred$diagnostic_summary()

$num_divergent
[1] 0 0

$num_max_treedepth
[1] 0 0

$ebfmi
[1] 1.104296 1.052395

参数的后验估计

fit_rongelap_poisson_pred$summary(variables = c("beta", "sigma", "phi"))

# A tibble: 3 × 10
  variable   mean median     sd     mad     q5    q95  rhat ess_bulk ess_tail
  <chr>     <num>  <num>  <num>   <num>  <num>  <num> <num>    <num>    <num>
1 beta     1.78   1.79   0.137  0.112   1.55   1.98    1.00    1917.    1072.
2 sigma    0.632  0.613  0.101  0.0797  0.514  0.801   1.00    1430.     954.
3 phi      0.0262 0.0233 0.0129 0.00788 0.0142 0.0465  1.00    1413.     993.

模型评估 LOO-CV

fit_rongelap_poisson_pred$loo(variables = "log_lik", cores = 2)

Warning: Some Pareto k diagnostic values are too high. See help('pareto-k-diagnostic') for details.

Computed from 2000 by 157 log-likelihood matrix

         Estimate  SE
elpd_loo   -937.2 4.1
p_loo       122.5 2.8
looic      1874.5 8.2
------
Monte Carlo SE of elpd_loo is NA.

Pareto k diagnostic values:
                         Count Pct.    Min. n_eff
(-Inf, 0.5]   (good)       0    0.0%   <NA>      
 (0.5, 0.7]   (ok)        21   13.4%   58        
   (0.7, 1]   (bad)      111   70.7%   9         
   (1, Inf)   (very bad)  25   15.9%   4         
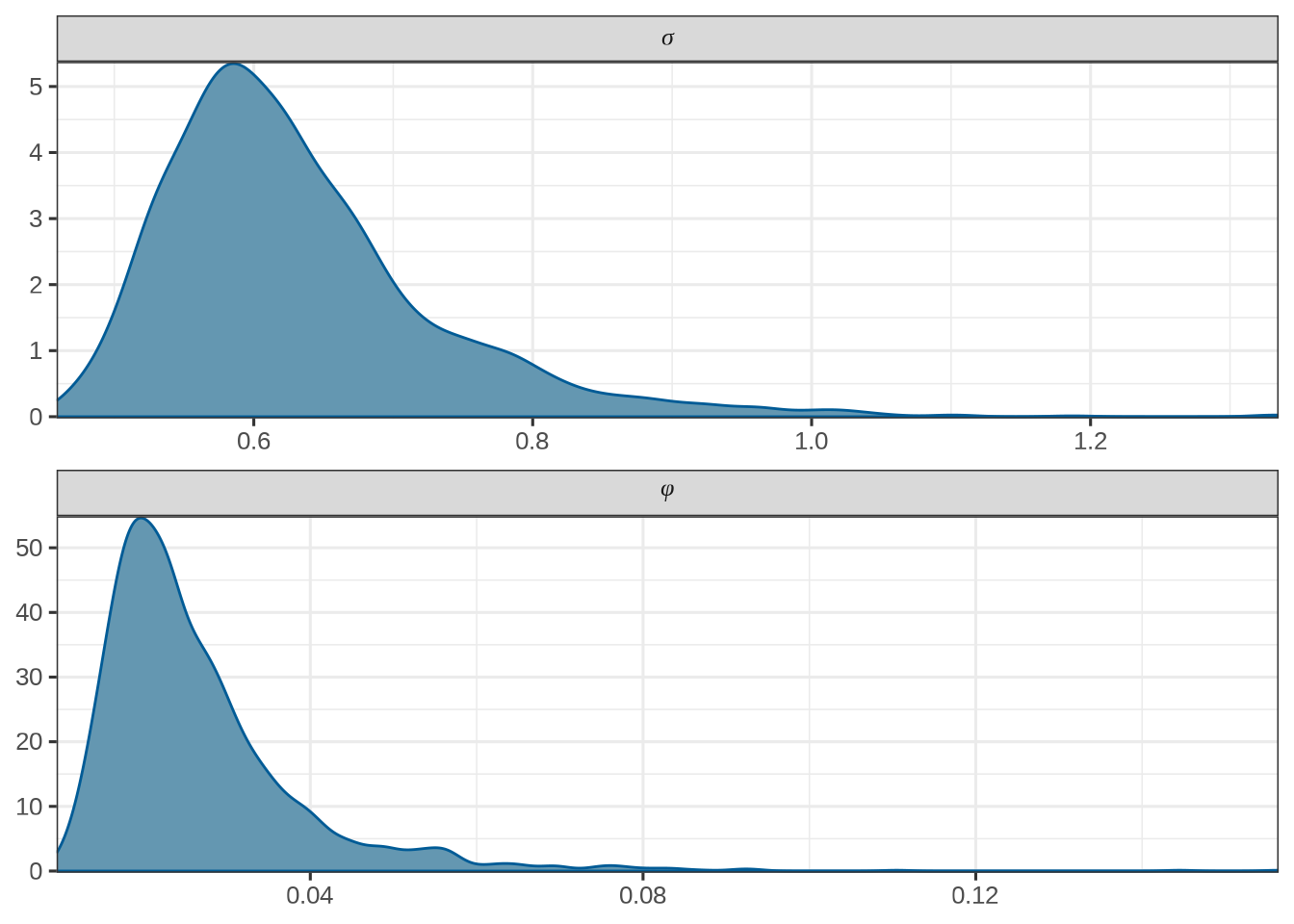
See help('pareto-k-diagnostic') for details.

检查辐射强度分布的拟合效果

# 抽取 yrep 数据
yrep <- fit_rongelap_poisson_pred$draws(variables = "yhat", format = "draws_matrix")
# Posterior predictive checks
pp_check(rongelap$counts / rongelap$time,
  yrep = sweep(yrep[1:50, ], MARGIN = 2, STATS = rongelap$time, FUN = `/`),
  fun = ppc_dens_overlay
) +
  theme_classic()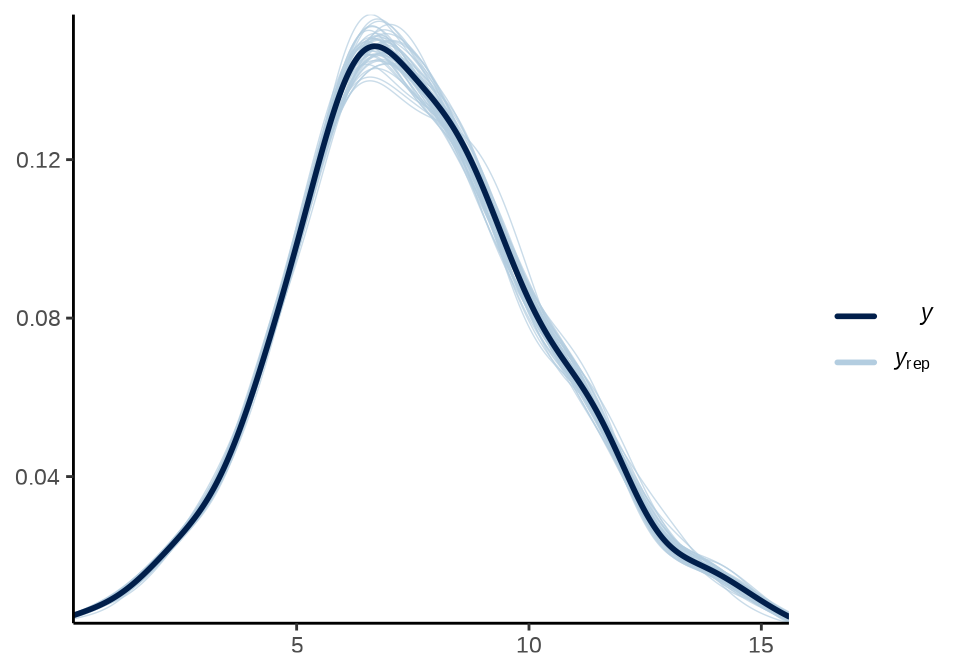

图 38.10: 后验预测诊断图（密度图）

后 1000 次迭代是平稳的，可取任意一个链条的任意一次迭代，获得采样点处的预测值

yhat_array <- fit_rongelap_poisson_pred$draws(variables = "yhat", format = "array")
lambda1_array <- fit_rongelap_poisson_pred$draws(variables = "lambda1", format = "array")
rongelap_sf$lambda <- as.vector(lambda1_array[1,1,])
rongelap_sf$yhat <- as.vector(yhat_array[1,1,])

数据集 rongelap_sf 的概况

rongelap_sf

Simple feature collection with 157 features and 4 fields
Geometry type: POINT
Dimension:     XY
Bounding box:  xmin: -6050 ymin: -3430 xmax: -50 ymax: 0
CRS:           NA
First 10 features:
   counts time            geometry   lambda yhat
1      75  300 POINT (-6050 -3270) -1.25962  116
2     371  300 POINT (-6050 -3165)  0.28423  414
3    1931  300 POINT (-5925 -3320)  1.81405 1867
4    4357  300 POINT (-5925 -3165)  2.66204 4324
5    2114  300 POINT (-5800 -3350)  1.89780 2045
6    2318  300 POINT (-5800 -3165)  2.04391 2405
7    1975  300 POINT (-5625 -3350)  1.91147 2068
8    1912  300 POINT (-5700 -3260)  1.84648 1859
9    1902  300 POINT (-5700 -3220)  1.80250 1766
10   1882  300 POINT (-5700 -3180)  1.83117 1886

观测值和预测值的情况

summary(rongelap_sf$counts / rongelap_sf$time)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  0.250   5.890   7.475   7.604   9.363  15.103 

summary(rongelap_sf$yhat / rongelap_sf$time)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
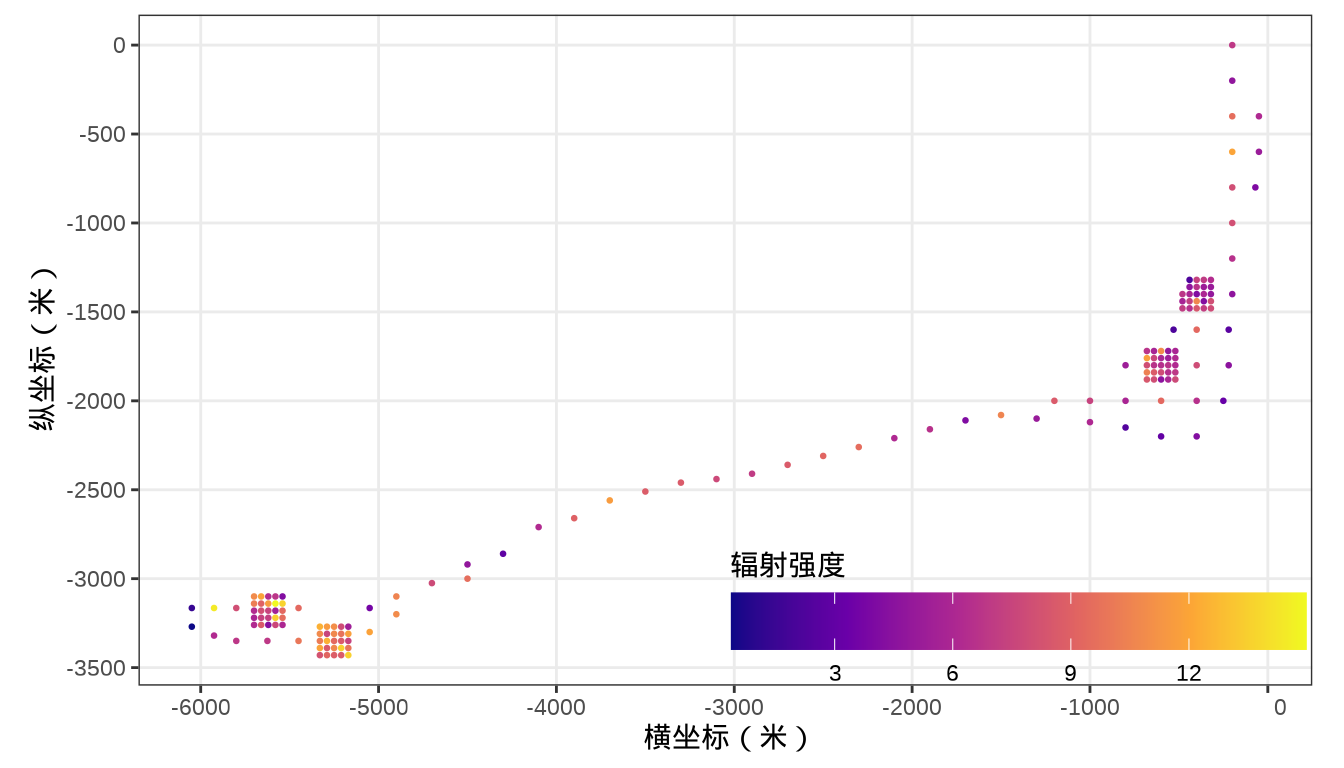
 0.3867  5.8867  7.3800  7.6088  9.3167 14.9700 

展示采样点处的预测值

代码

ggplot(data = rongelap_sf)+
  geom_sf(aes(color = yhat / time), cex = 0.5) +
  scale_colour_viridis_c(option = "C", breaks = 3*0:5,
    guide = guide_colourbar(
      barwidth = 15, barheight = 1.5,
      title.position = "top" # 图例标题位于图例上方
    )) +
  theme_bw() +
  labs(x = "横坐标（米）", y = "纵坐标（米）", colour = "辐射强度") +
  theme(
    legend.position = c(0.75, 0.1),
    legend.direction = "horizontal",
    legend.background = element_blank()
  )

图 38.11: 朗格拉普岛核辐射强度的分布

未采样点的预测

# 后验估计
ypred_tbl <- fit_rongelap_poisson_pred$summary(variables = "ypred", "mean")
rongelap_grid_df$ypred <- ypred_tbl$mean
# 查看预测结果
head(rongelap_grid_df)

         cX        cY time    ypred
1 -5685.942 -3606.997  100 741.1470
2 -5643.145 -3606.997  100 750.2260
3 -5600.347 -3606.997  100 759.1190
4 -5557.549 -3606.997  100 777.9825
5 -5514.751 -3606.997  100 779.8040
6 -5471.953 -3606.997  100 790.0260

# 预测值的分布范围
summary(rongelap_grid_df$ypred / rongelap_grid_df$time)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
 0.4978  6.2022  7.3942  7.3081  8.5636 12.9960 

转化数据类型，去掉缓冲区内的预测位置，准备绘制辐射强度预测值的分布

rongelap_grid_sf <- st_as_sf(rongelap_grid_df, coords = c("cX", "cY"), dim = "XY")
rongelap_grid_stars <- st_rasterize(rongelap_grid_sf, nx = 150, ny = 75)
rongelap_stars <- st_crop(x = rongelap_grid_stars, y = rongelap_coastline_sfp)

代码

# 虚线框数据
dash_sfp <- st_polygon(x = list(rbind(
  c(-6000, -3600),
  c(-6000, -2600),
  c(-5000, -2600),
  c(-5000, -3600),
  c(-6000, -3600)
)), dim = "XY")
# 主体内容
p3 <- ggplot() +
  geom_stars(
    data = rongelap_stars, na.action = na.omit,
    aes(fill = ypred / time)
  ) +
  # 海岸线
  geom_sf(
    data = rongelap_coastline_sfp,
    fill = NA, color = "gray30", linewidth = 0.5
  ) +
  # 图例
  scale_fill_viridis_c(
    option = "C", breaks = 0:13,
    guide = guide_colourbar(
      barwidth = 15, barheight = 1.5,
      title.position = "top" # 图例标题位于图例上方
    )
  ) +
  # 虚线框
  geom_sf(data = dash_sfp, fill = NA, linewidth = 0.75, lty = 2) +
  # 箭头
  geom_segment(
    data = data.frame(x = -5500, xend = -5000, y = -2600, yend = -2250),
    aes(x = x, y = y, xend = xend, yend = yend),
    arrow = arrow(length = unit(0.03, "npc"))
  ) +
  theme_bw() +
  labs(x = "横坐标（米）", y = "纵坐标（米）", fill = "辐射强度") +
  theme(
    legend.position = c(0.75, 0.1),
    legend.direction = "horizontal",
    legend.background = element_blank()
  )

p4 <- ggplot() +
  geom_stars(
    data = rongelap_stars, na.action = na.omit,
    aes(fill = ypred / time), show.legend = FALSE
  ) +
  geom_sf(
    data = rongelap_coastline_sfp,
    fill = NA, color = "gray30", linewidth = 0.75
  ) +
  scale_fill_viridis_c(option = "C", breaks = 0:13) +
  # 虚线框
  geom_sf(data = dash_sfp, fill = NA, linewidth = 0.75, lty = 2) +
  theme_void() +
  coord_sf(expand = FALSE, xlim = c(-6000, -5000), ylim = c(-3600, -2600))
# 叠加图形
p3
print(p4, vp = grid::viewport(x = .3, y = .65, width = .45, height = .45))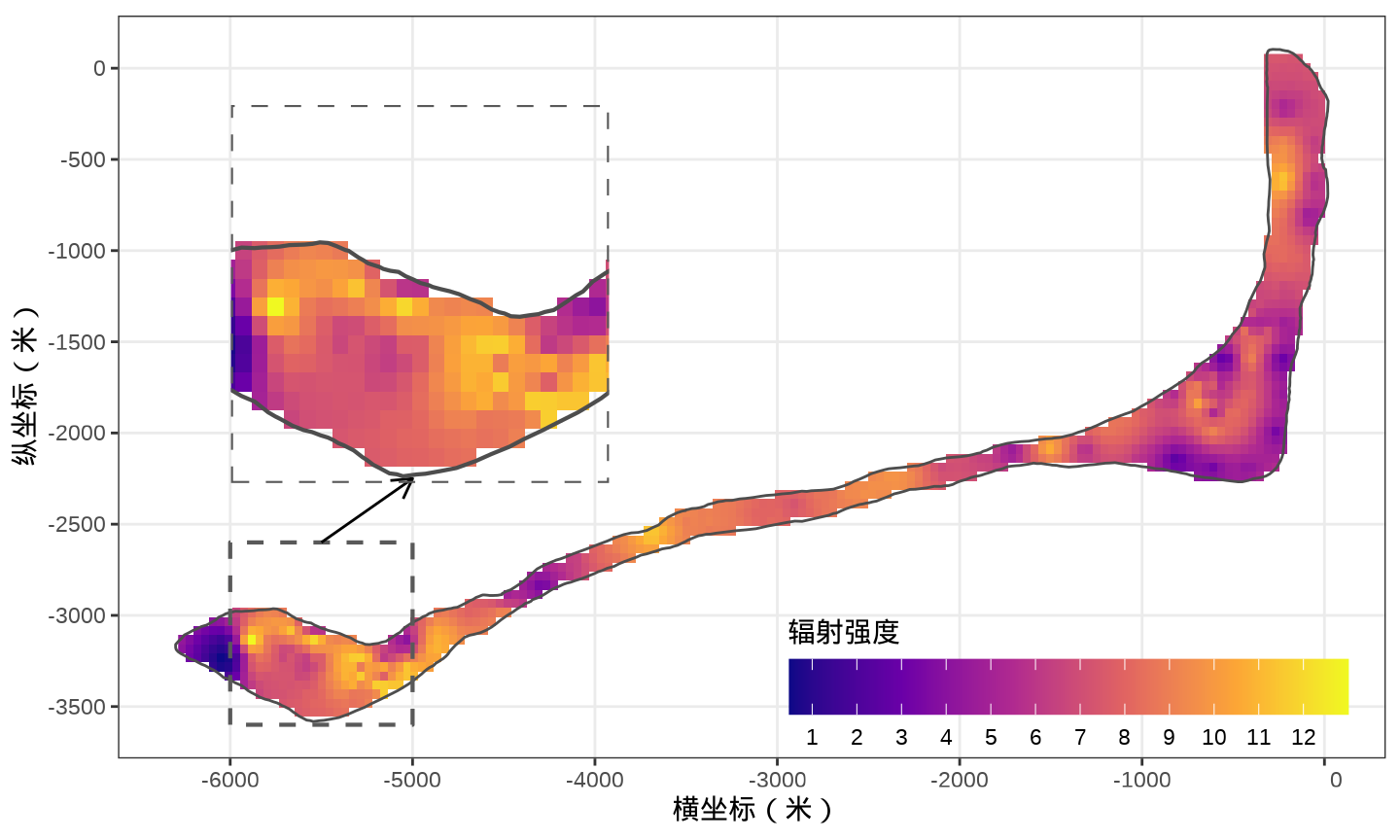

图 38.12: 朗格拉普岛核辐射强度的分布

38.4 总结

从模型是否含有块金效应、不同的自相关函数和参数估计方法等方面比较。

library(nlme)
# 高斯分布、指数型自相关结构
fit_exp_reml <- gls(log(counts / time) ~ 1,
  correlation = corExp(value = 200, form = ~ cX + cY, nugget = FALSE),
  data = rongelap, method = "REML"
)
fit_exp_ml <- gls(log(counts / time) ~ 1,
  correlation = corExp(value = 200, form = ~ cX + cY, nugget = FALSE),
  data = rongelap, method = "ML"
)
fit_exp_reml_nugget <- gls(log(counts / time) ~ 1,
  correlation = corExp(value = c(200, 0.1), form = ~ cX + cY, nugget = TRUE),
  data = rongelap, method = "REML"
)
fit_exp_ml_nugget <- gls(log(counts / time) ~ 1,
  correlation = corExp(value = c(200, 0.1), form = ~ cX + cY, nugget = TRUE),
  data = rongelap, method = "ML"
)

# 高斯分布、高斯型自相关结构
fit_gaus_reml <- gls(log(counts / time) ~ 1,
  correlation = corGaus(value = 200, form = ~ cX + cY, nugget = FALSE),
  data = rongelap, method = "REML"
)
fit_gaus_ml <- gls(log(counts / time) ~ 1,
  correlation = corGaus(value = 200, form = ~ cX + cY, nugget = FALSE),
  data = rongelap, method = "ML"
)
fit_gaus_reml_nugget <- gls(log(counts / time) ~ 1,
  correlation = corGaus(value = c(200, 0.1), form = ~ cX + cY, nugget = TRUE),
  data = rongelap, method = "REML"
)
fit_gaus_ml_nugget <- gls(log(counts / time) ~ 1,
  correlation = corGaus(value = c(200, 0.1), form = ~ cX + cY, nugget = TRUE),
  data = rongelap, method = "ML"
)

汇总结果见下表。

表格 38.1: 不同模型与参数估计方法的比较

响应变量分布	空间自相关结构	块金效应	估计方法	\(\beta\)	\(\sigma^2\)	\(\phi\)	对数似然值
高斯分布	指数型	无	REML	1.826	0.3172	110.8	-89.07
高斯分布	指数型	无	ML	1.828	0.3064	105.4	-87.56
高斯分布	指数型	0.03598	REML	1.813	0.2935	169.7472	-88.22
高斯分布	指数型	0.03312	ML	1.828	0.2779	150.1324	-86.88
高斯分布	高斯型	无	REML	1.878	0.2523	41.96	-100.7
高斯分布	高斯型	无	ML	1.879	0.25	41.81	-98.62
高斯分布	高斯型	0.07055	REML	1.831	0.2532	139.1431	-84.91
高斯分布	高斯型	0.07053	ML	1.832	0.2459	137.0980	-83.32

相比于其他参数，REML 和 ML 估计方法对参数 \(\phi\) 影响很大，ML 估计的 \(\phi\) 和对数似然函数值更大。高斯型自相关结构中，REML 和 ML 估计方法对参数 \(\phi\) 的估计结果差不多。函数 gls() 对初值要求不高，以上初值选取比较随意，只是符合要求函数定义。

对普通用户来说，想要流畅地使用 Stan 框架，需要面对很多挑战。

1. 软件安装和配置过程复杂。rstan 包内置的 Stan 版本远低于最新发布的 Stan 版本，编译工具，rstan 终于要发布新版本了。
2. 编译和运行模型的参数控制选项很多。编译模型，OpenCL 和多线程支持，HMC（NUTS）、L-BFGS 和 VI 三大推理算法的参数设置
3. 模型参数先验分布设置技巧高。模型参数的先验对数据的依赖非常高，仅对线性和广义线性模型依赖较小。即使是面对模拟的简单广义线性混合效应模型，抽样过程也发散严重。
4. 面对大规模数据扩展困难。以朗格拉普岛的核污染预测任务为例，处理 157 维的积分显得非常吃力，对 1600 个参数的后验分布模拟和推断非常低效。

2020 年 Stan 大会 Wade Brorsen 介绍采用 Stan 实现的贝叶斯克里金（Kriging）平滑算法估计和预测各郡县的作物产量。Stan 实现的贝叶斯空间分层正态模型，回归参数随空间区域位置变化，参数的先验分布与空间区域相关，引入大量带超参数的先验分布，运行效率不高，跑模型花费很多时间。假定所有的参数随空间位置变化，模型参数个数瞬间爆炸，跑模型花费 31 天 (Niyizibi, Brorsen, 和 Park 2018)。

Stan 总有些优势吧！

• Stan 非常灵活。Stan 同时是一门概率编程语言，只要统计模型可以被 Stan 编码，理论上就可以编译、运行、获得结果。
• Stan 功能很多。Stan 还可以解刚性的常微分方程、积分方程等。 非常灵活，非常适合学术研究工作者，计算层面，可以方便地在前人的工作上扩展。
• Stan 文档很全。函数手册 提供 Stan 内建的各类函数说明。编程手册 提供 Stan 编程语法、程序块的说明，教用户如何使用 Stan 写代码。用户手册 提供 Stan 支持的各类统计模型、代数和微分方程的使用示例。

38.5 习题

1. 对核辐射污染数据，建立对数高斯过程模型，用 Stan 编码模型，预测全岛的核辐射强度分布。

   \[ \begin{aligned} \beta &\sim \mathrm{std\_normal}(0,1) \\ \sigma &\sim \mathrm{inv\_gamma}(5,5) \\ \phi &\sim \mathrm{half\_std\_normal}(0,1) \\ \tau &\sim \mathrm{half\_std\_normal}(0,1) \\ \bm{y} &\sim \mathrm{multivariate\_normal}(\bm{\beta}, \sigma^2 \Sigma+ \tau^2 I) \end{aligned} \]

   其中，\(\beta\) 代表截距，先验分布为标准正态分布，\(\sigma\) 代表高斯过程的方差参数（信号），先验分布为逆伽马分布，\(\phi\) 代表高斯过程的范围参数，先验分布为半标准正态分布，\(y\) 代表辐射强度的对数，给定参数和数据的条件分布为多元正态分布，\(\Sigma\) 代表协方差矩阵，\(I\) 代表与采样点数量相同的单位矩阵， \(\tau^2\) 是块金效应。

   functions {
     vector gp_pred_rng(array[] vector x2,
                        vector y1,
                        array[] vector x1,
                        real sigma,
                        real phi,
                        real tau,
                        real delta) {
       int N1 = rows(y1);
       int N2 = size(x2);
       vector[N2] f2;
       {
         matrix[N1, N1] L_K;
         vector[N1] K_div_y1;
         matrix[N1, N2] k_x1_x2;
         matrix[N1, N2] v_pred;
         vector[N2] f2_mu;
         matrix[N2, N2] cov_f2;
         matrix[N2, N2] diag_delta;
         matrix[N1, N1] K;
         K = gp_exponential_cov(x1, sigma, phi);
         for (n in 1:N1) {
           K[n, n] = K[n, n] + square(tau);
         }
         L_K = cholesky_decompose(K);
         K_div_y1 = mdivide_left_tri_low(L_K, y1);
         K_div_y1 = mdivide_right_tri_low(K_div_y1', L_K)';
         k_x1_x2 = gp_exponential_cov(x1, x2, sigma, phi);
         f2_mu = (k_x1_x2' * K_div_y1);
         v_pred = mdivide_left_tri_low(L_K, k_x1_x2);
         cov_f2 = gp_exponential_cov(x2, sigma, phi) - v_pred' * v_pred;
         diag_delta = diag_matrix(rep_vector(delta, N2));
   
         f2 = multi_normal_rng(f2_mu, cov_f2 + diag_delta);
       }
       return f2;
     }
   }
   data {
     int<lower=1> D;
     int<lower=1> N1;
     array[N1] vector[D] x1;
     vector[N1] y1;
     int<lower=1> N2;
     array[N2] vector[D] x2;
   }
   transformed data {
     real delta = 1e-9;
   }
   parameters {
     real beta;
     real<lower=0> phi;
     real<lower=0> sigma;
     real<lower=0> tau;
   }
   transformed parameters {
     vector[N1] mu = rep_vector(beta, N1);
   }
   model {
     matrix[N1, N1] L_K;
     {
       matrix[N1, N1] K = gp_exponential_cov(x1, sigma, phi);
       real sq_tau = square(tau);
   
       // diagonal elements
       for (n1 in 1:N1) {
         K[n1, n1] = K[n1, n1] + sq_tau;
       }
   
       L_K = cholesky_decompose(K);
     }
   
     beta ~ std_normal();
     phi ~ std_normal();
     sigma ~ inv_gamma(5, 5);
     tau ~ std_normal();
   
     y1 ~ multi_normal_cholesky(mu, L_K);
   }
   generated quantities {
     vector[N2] f2;
     vector[N2] ypred;
   
     f2 = gp_pred_rng(x2, y1, x1, sigma, phi, tau, delta);
     for (n2 in 1:N2) {
       ypred[n2] = normal_rng(f2[n2], tau);
     }
   }

   代码中，gp_exponential_cov 表示空间相关性结构选择了指数型，详见 Stan 函数手册中的指数型核函数表示。cholesky_decompose 表示对协方差矩阵做 Cholesky 分解，分解出来的下三角矩阵作为多元正态分布的参数，详见 Stan 函数手册中的 Cholesky 分解。 multi_normal_cholesky 表示基于 Cholesky 分解的多元正态分布。详见 Stan 函数手册中的多元正态分布的 Cholesky 参数化表示。

   代码

   set.seed(20232023)
   nchains <- 2 # 2 条迭代链
   # 给每条链设置不同的参数初始值
   inits_data_gaussian <- lapply(1:nchains, function(i) {
     list(
       beta = rnorm(1),
       sigma = runif(1),
       phi = runif(1),
       tau = runif(1)
     )
   })
   
   # 对数高斯模型
   rongelap_gaussian_d <- list(
     N1 = nrow(rongelap), # 观测记录的条数
     N2 = nrow(rongelap_grid_df),
     D = 2, # 2 维坐标
     x1 = rongelap[, c("cX", "cY")] / 6000, # N x 2 坐标矩阵
     x2 = rongelap_grid_df[, c("cX", "cY")] / 6000,
     y1 = log(rongelap$counts / rongelap$time) # N 向量
   )
   # 编码
   mod_rongelap_gaussian <- cmdstan_model(
     stan_file = "code/gaussian_process_pred.stan",
     compile = TRUE, cpp_options = list(stan_threads = TRUE)
   )
   
   # 对数高斯模型
   fit_rongelap_gaussian <- mod_rongelap_gaussian$sample(
     data = rongelap_gaussian_d,   # 观测数据
     init = inits_data_gaussian,   # 迭代初值
     iter_warmup = 500,            # 每条链预处理迭代次数
     iter_sampling = 1000,         # 每条链总迭代次数
     chains = nchains,             # 马尔科夫链的数目
     parallel_chains = 2,      # 指定 CPU 核心数，可以给每条链分配一个
     threads_per_chain = 1,    # 每条链设置一个线程
     show_messages = FALSE,    # 不显示迭代的中间过程
     refresh = 0,              # 不显示采样的进度
     output_dir = "data-raw/",
     seed = 20232023           # 设置随机数种子，不要使用 set.seed() 函数
   )
   
   # 诊断
   fit_rongelap_gaussian$diagnostic_summary()
   # 对数高斯模型
   fit_rongelap_gaussian$summary(
     variables = c("lp__", "beta", "sigma", "phi", "tau"),
     .num_args = list(sigfig = 4, notation = "dec")
   )
   
   # 未采样的位置的核辐射强度预测值
   ypred <- fit_rongelap_gaussian$summary(variables = "ypred", "mean")
   # 预测值
   rongelap_grid_df$ypred <- exp(ypred$mean)
   # 整理数据
   rongelap_grid_sf <- st_as_sf(rongelap_grid_df, coords = c("cX", "cY"), dim = "XY")
   rongelap_grid_stars <- st_rasterize(rongelap_grid_sf, nx = 150, ny = 75)
   rongelap_stars <- st_crop(x = rongelap_grid_stars, y = rongelap_coastline_sfp)
   
   # 虚线框数据
   dash_sfp <- st_polygon(x = list(rbind(
     c(-6000, -3600),
     c(-6000, -2600),
     c(-5000, -2600),
     c(-5000, -3600),
     c(-6000, -3600)
   )), dim = "XY")
   # 主体内容
   p3 <- ggplot() +
     geom_stars(
       data = rongelap_stars, na.action = na.omit,
       aes(fill = ypred)
     ) +
     # 海岸线
     geom_sf(
       data = rongelap_coastline_sfp,
       fill = NA, color = "gray30", linewidth = 0.5
     ) +
     # 图例
     scale_fill_viridis_c(
       option = "C", breaks = 0:12,
       guide = guide_colourbar(
         barwidth = 15, barheight = 1.5,
         title.position = "top" # 图例标题位于图例上方
       )
     ) +
     # 虚线框
     geom_sf(data = dash_sfp, fill = NA, linewidth = 0.75, lty = 2) +
     # 箭头
     geom_segment(
       data = data.frame(x = -5500, xend = -5000, y = -2600, yend = -2250),
       aes(x = x, y = y, xend = xend, yend = yend),
       arrow = arrow(length = unit(0.03, "npc"))
     ) +
     theme_bw() +
     labs(x = "横坐标（米）", y = "纵坐标（米）", fill = "辐射强度") +
     theme(
       legend.position = c(0.75, 0.1),
       legend.direction = "horizontal",
       legend.background = element_blank()
     )
   
   p4 <- ggplot() +
     geom_stars(
       data = rongelap_stars, na.action = na.omit,
       aes(fill = ypred), show.legend = FALSE
     ) +
     geom_sf(
       data = rongelap_coastline_sfp,
       fill = NA, color = "gray30", linewidth = 0.75
     ) +
     scale_fill_viridis_c(option = "C", breaks = 0:12) +
     # 虚线框
     geom_sf(data = dash_sfp, fill = NA, linewidth = 0.75, lty = 2) +
     theme_void() +
     coord_sf(expand = FALSE, xlim = c(-6000, -5000), ylim = c(-3600, -2600))
   # 叠加图形
   p3
   print(p4, vp = grid::viewport(x = .3, y = .65, width = .45, height = .45))

Diggle, P. J., J. A. Tawn, 和 R. A. Moyeed. 1998. 《Model-based geostatistics》. Journal of the Royal Statistical Society: Series C (Applied Statistics) 47 (3): 299–350. https://doi.org/10.1111/1467-9876.00113.

Niyizibi, Bart, Wade Brorsen, 和 Eunchun Park. 2018. 《Using Bayesian Kriging for Spatial Smoothing of Trends in the Means and Variances of Crop Yield Densities》. Economic Geography. https://doi.org/10.22004/ag.econ.274403.